许多高级语言中都提供有排序函数,但是掌握一些经典排序算法的基本原理和编码方法还是很有必要,这个学习过程可以帮助我们更好的理解每种排序算法的设计思路。
一、直接插入排序
直接插入排序是最简单的一种排序算法,也最容易理解。它的核心思想为将元素逐个插入一个有序的数列中。用文字描述可以分为如下几步:
1.把数列中的第一个元素取出,作为有序数列的起始元素。
2.依次拿数列中的其他元素与有序数列中的元素进行比较,将其插入正确的位置。
用图示描述插入排序如下:
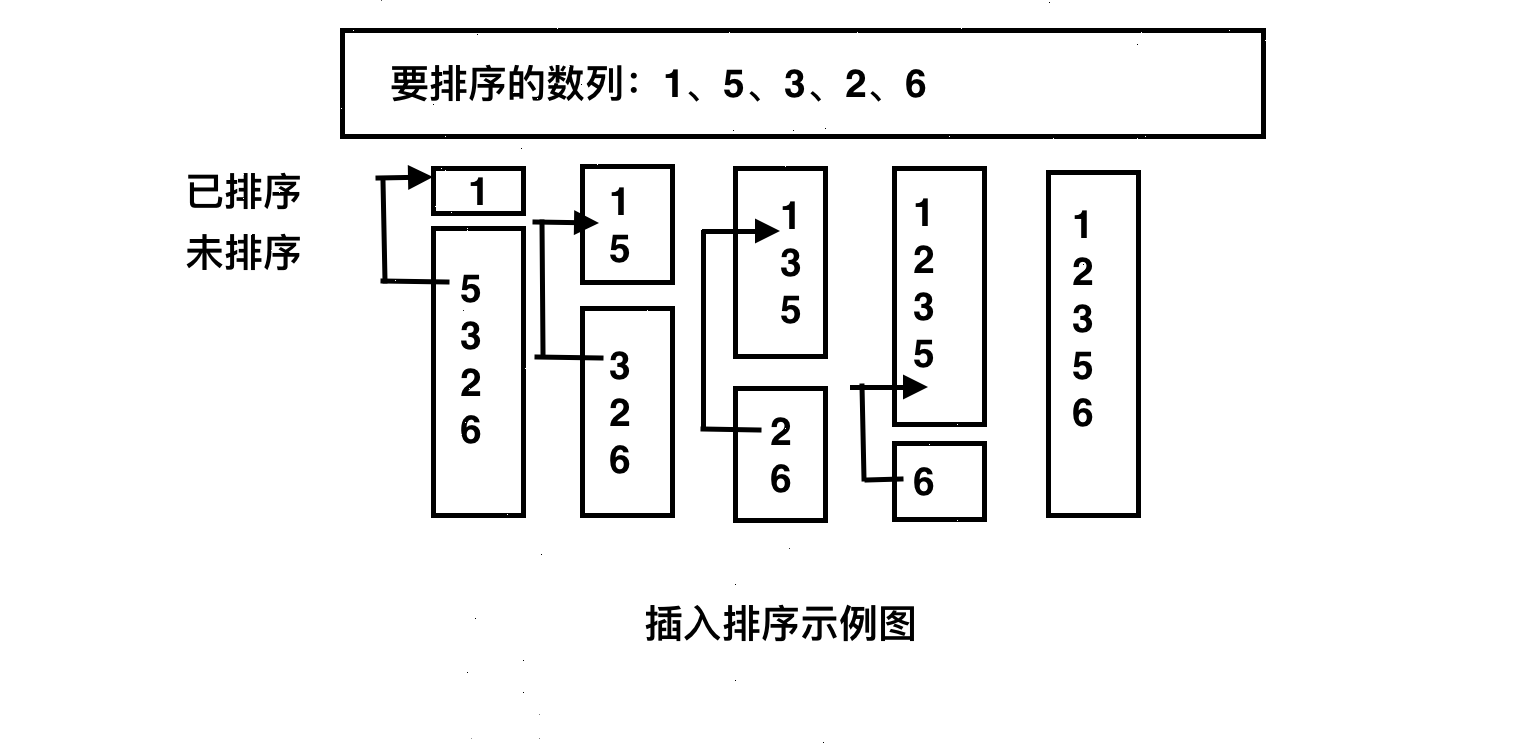
直接插入排序的特点是对新元素的每轮插入前,有序数列中的所有元素都是排序好的,即任意时刻,被排序动过的元素组成的数列都是有序的。
用C实现的简单插入排序:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
| #include <stdio.h>
void mySort(int array[],int size){
for(int i=0;i<size-1;i++){
int temp = array[i+1];
for(int j=i+1;j>0;j--){
if(temp<array[j]){
array[j+1] = array[j];
array[j] = temp;
}
}
}
}
int main(){
int a[] = {1, 2, 12, 34, 46, 54, 64, 65, 76, 98 };
mySort(a,10);
for(int i = 0;i<10;i++){
printf("%d\n",a[i]);
}
return 0;
}
|
二、二分插入排序(折半插入排序)
二分插入排序也是插入排序的一种,其又叫做折半插入排序。它与直接插入排序的唯一不同只在于查找插入位置的方式。直接插入排序是通过遍历来查找要插入元素的位置,二分插入排序则是通过二分法来查找要插入的位置,之后将此位置所有元素后移,将排序的元素进行插入。
C实现的二分插入排序:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
| #include <stdio.h>
void mySort(int array[],int size){
for(int i=0;i<size-1;i++){
int temp = array[i+1];
int left=0,right=i,middle;
while(left<=right){
middle = (left+right)/2;
if(array[middle]>temp){
right=middle-1;
}else {
left = middle+1;
}
}
for(int j =i+1;j>left;j--){
array[j] = array[j-1];
}
array[left] = temp;
}
}
int main(){
int a[] = {1, 2, 12, 34, 46, 54, 64, 65, 76, 98 };
mySort(a,10);
for(int i = 0;i<10;i++){
printf("%d\n",a[i]);
}
return 0;
}
|
三、希尔排序
希尔排序也是插入排序的一种,它先将整个数列分割成若干个小的子序列进行插入排序,逐渐减少子序列的个数,直到最后组合成一个数列,完成整个排序过程。希尔排序的过程使用文字描述可以表示为如下几步:
1.假设数列元素个数为n,先取一个小于n的增量d1,将所有间隔d1距离的元素放为1组进行插入排序,d1通常取值n/2,向下取整。
2.再次取d2<d1,将所有间隔d2距离的元素放为1组进行插入排序,通常d2取值为d1/2,向下取整。
3.重复步骤2,直到取得d等于1。
图示希尔排序如下: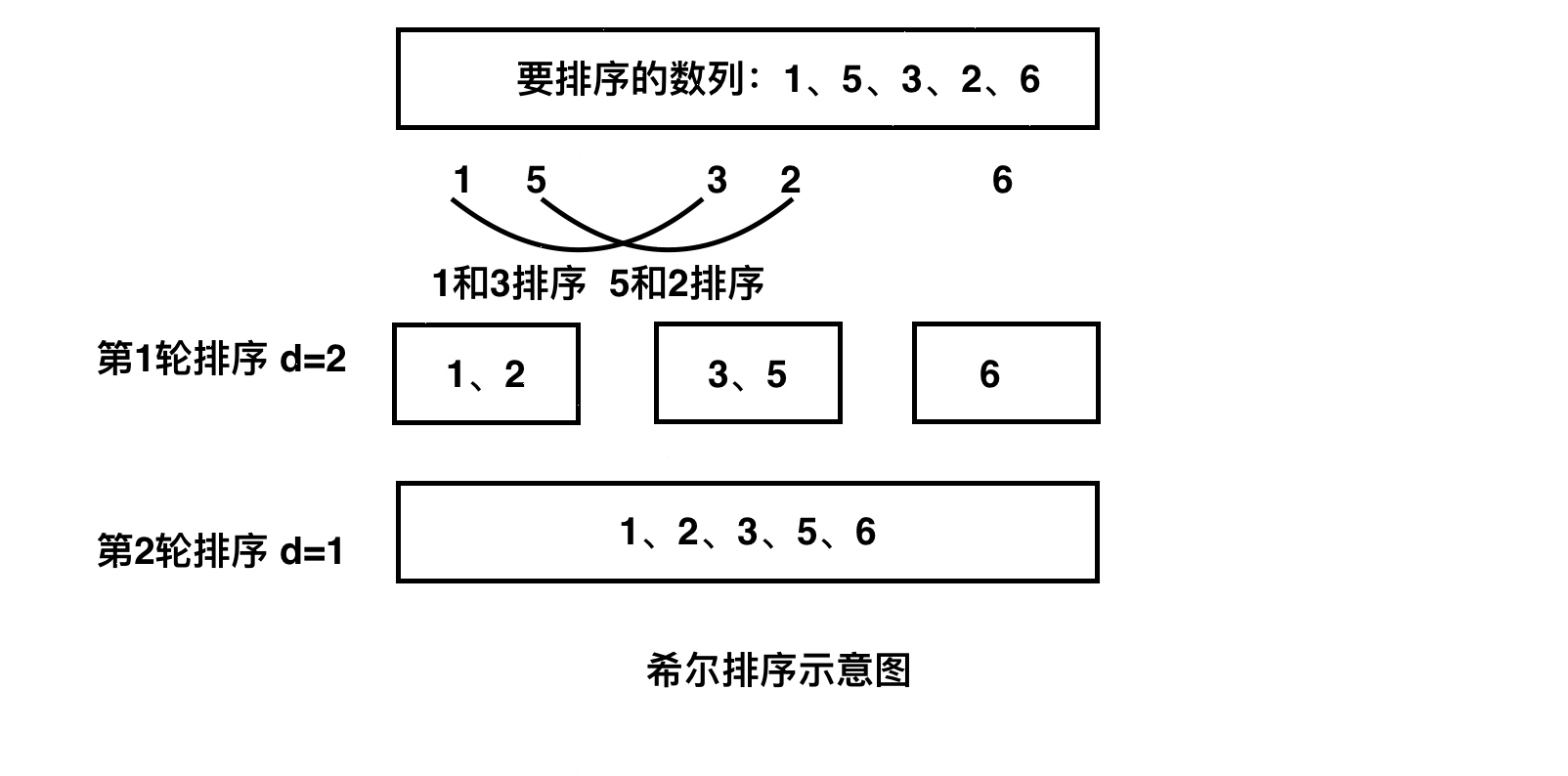
C实现的希尔排序:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
| #include <stdio.h>
void mySort(int array[],int size){
int d = size/2;
while(d>=1){
int counts = size/d;
for (int i = 0; i < d ; i++) {
for(int j = 0;j<counts-1;j++){
int temp = array[(j+1)*d];
for(int k = ((j+1)*d);k>0;k-=d){
if (temp<array[k]) {
array[k+d] = array[k];
array[k] = temp;
}
}
}
}
d=d/2;
}
}
int main(){
int a[] = {1, 2, 12, 34, 46, 54, 64, 65, 76, 98 };
mySort(a,10);
for(int i = 0;i<10;i++){
printf("%d\n",a[i]);
}
return 0;
}
|
四、选择排序
前边所说的3种排序算法原理上都是插入排序,即从无序数列中逐个取元素将其插入到有序数列中的合适位置。选择排序则刚好与之相反,其从无序数列中先找到最小值,放在排序数列首部,在依次找到剩余数列的中最小值追加入有序数列,最终完成数列的排序。用文字描述选择排序步骤不如:
1.找到数列中的最小值,将其作为有序数列的第一个元素。
2.从剩余数列中找到最小值,追加入有序数列。
3.重复步骤2,直到排完整个数列。
图示描述选择排序如下: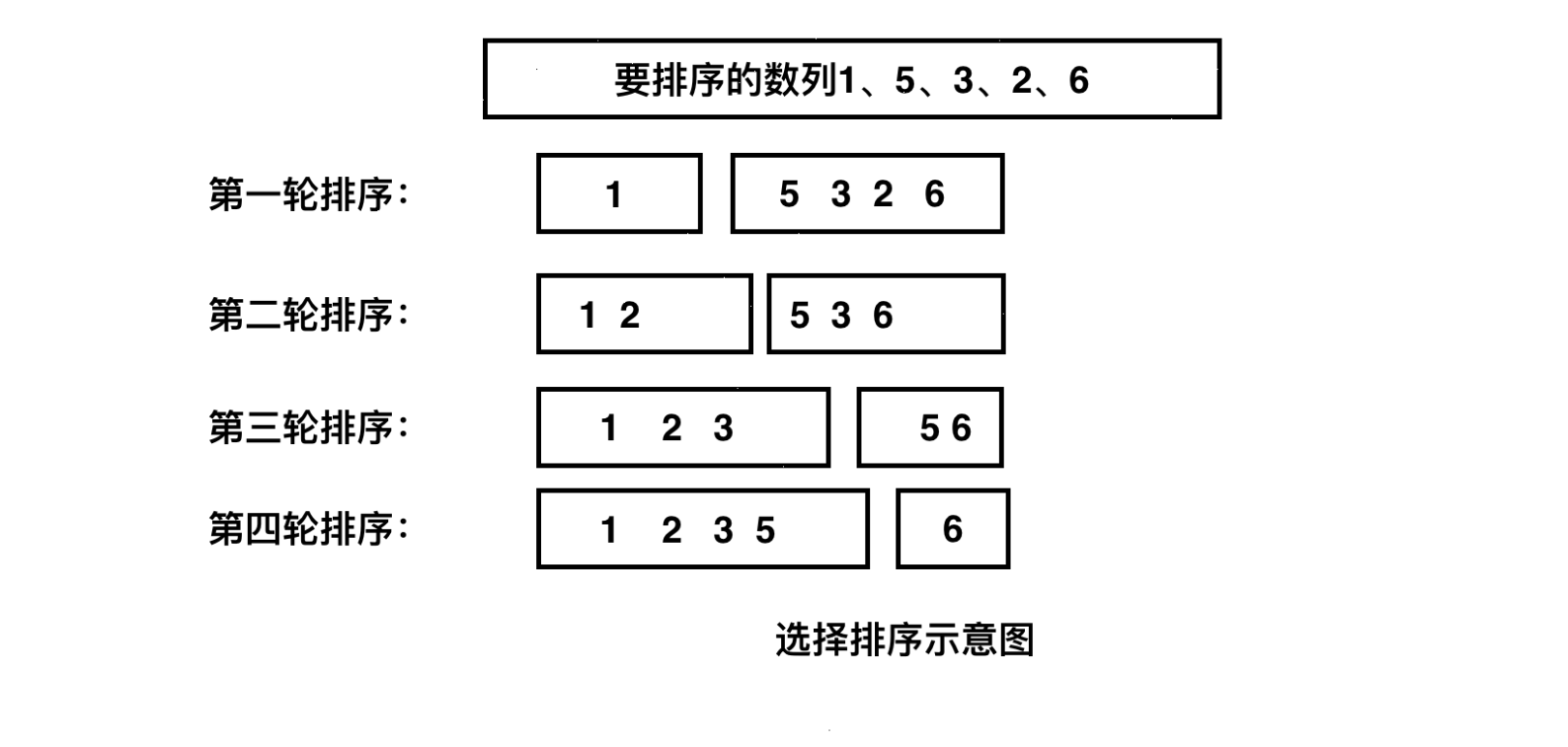
C实现的选择排序算法:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
|
void mySort(int array[],int size){
for(int i=0;i<size-1;i++){
int min = array[i];
int index = i;
for(int j=i+1;j<size;j++){
if(array[j]<min){
min = array[j];
index = j;
}
}
array[index] = array[i];
array[i]=min;
}
}
int main(){
int a[] = {1, 2, 12, 34, 46, 54, 64, 65, 76, 98};
mySort(a,11);
for(int i = 0;i<10;i++){
printf("%d\n",a[i]);
}
return 0;
}
|
五、冒泡排序
冒泡排序和选择排序是我们学习编程课时必不可少的两种排序算法,冒泡排序算法的核心是每次比较相邻的连个元素,如果它们的顺序不对,则进行交换,一轮排序下来,最大值一定被排序到数列的末端。之后除去最后一个元素再进行第二轮冒泡,直到整个数列排序完成。用文字描述冒泡排序的过程如下:
1.从左向右依次比较相邻两元素,如果顺序不对,则进行交换,最终最大的元素被放在最后。
2.除去最后一个元素,重复步骤1,最终剩下元素中最大的被放在倒数第2个位置。
3.继续上面的重复,直到排完整个数列。
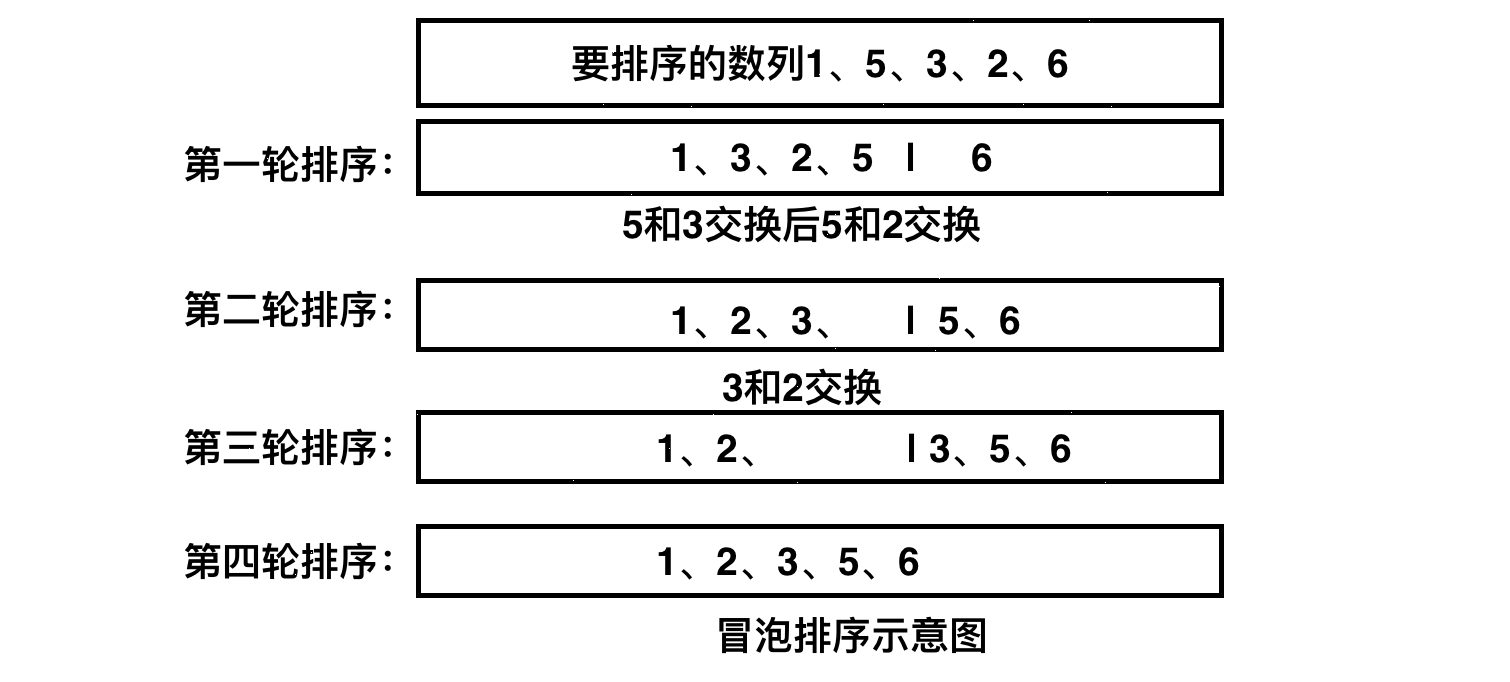
C实现的冒泡排序算法:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
| #include <stdio.h>
void mySort(int array[],int size){
for(int i =0;i<size-1;i++){
for(int j=0;j<size-1-i;j++){
int temp = array[j];
if(temp>array[j+1]){
array[j] = array[j+1];
array[j+1] = temp;
}
}
}
}
int main(){
int a[] = {1, 2, 12, 34, 46, 54, 64, 65, 76, 98};
mySort(a,10);
for(int i = 0;i<10;i++){
printf("%d\n",a[i]);
}
return 0;
}
|
六、双向冒泡排序
双向冒泡排序是冒泡排序的一种变体,冒泡排序每次比较都是从左向右,找出最大的放在最后。双向冒泡排序则是第一轮从左向右将最大的放最后,第二轮从右向左将最小的放最首,如此交替直到整个数列排序完成。文字描述双向冒泡排序步骤如下:
1.从左向右依次比较相邻两个元素,如果顺序不对,则进行交换,如此一轮下来,最大的元素在最后。
2.除去已经排序好的元素,从右向左依次比较相邻的两个元素,如果顺序不对,则进行交换,最小的元素在首部。
3.交替重复步骤1与步骤2直到排序完成。
双向冒泡排序示意图如下:
C实现的双向冒泡排序算法:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
| #include <stdio.h>
void mySort(int array[],int size){
int start = 0;
int end = size;
for(int i=start;i<end-1;i++){
int temp = array[i];
if (array[i+1]<temp) {
array[i] = array[i+1];
array[i+1] = temp;
}
}
end--;
for(int j=end;j>start+1;j--){
int temp = array[j];
if (array[j-1]>temp) {
array[j] = array[j-1];
array[j-1] = temp;
}
}
start++;
}
int main(){
int a[] = {1, 2, 12, 34, 46, 54, 64, 65, 76, 98,33};
mySort(a,11);
for(int i = 0;i<11;i++){
printf("%d\n",a[i]);
}
return 0;
}
|
七、快速排序算法
快速排序算法和基本思路是通过一趟排序将数列分成两部分,其中一部分的所有数据都比另一部分小。之后在分别在两个子数列中进行递归,直到最终排序完成。快速排序算法的核心是递归,因此其效率十分高。用文字描述快速排序的步骤如下:
1.随机取一个元素作为基准,将小于此元素的数据都放在此元素的左侧,大于此元素的数据都放在此元素的右侧,将数列分隔成左右两个子数列。
2.分别对左右子数列进行步骤1的递归,直到数列长度为1或者0,表示排序完成。
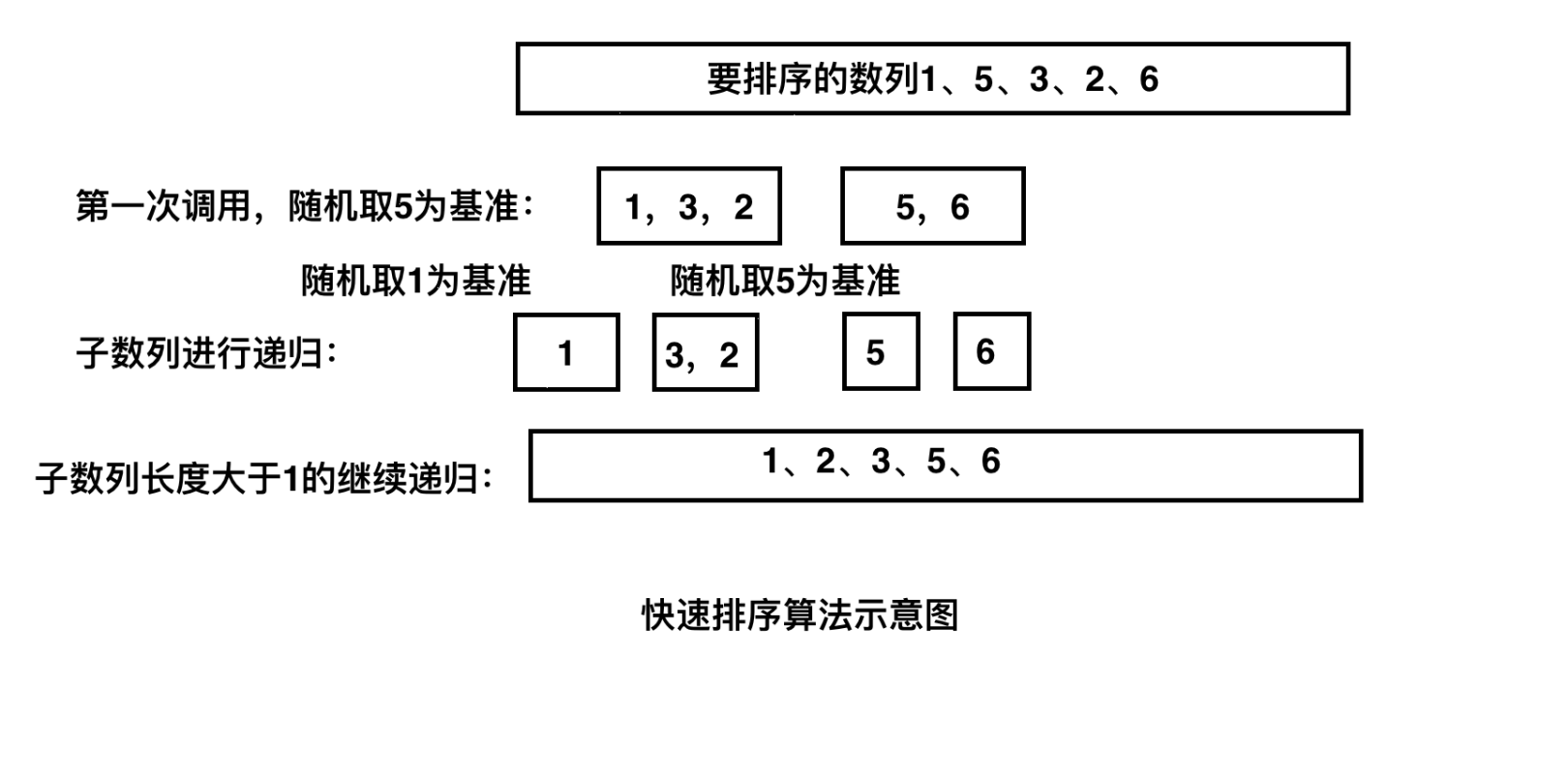
C语言实现的快速排序:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
| #include <stdio.h>
void mySort(int array[],int left,int right){
if(right-left>=1){
int base = array[left];
int i = left+1;
int index = left;
while(i<=right){
if(array[i]<base){
if(index+1==i){
array[index] = array[i];
array[i]=base;
index = i;
}else{
array[index]=array[index+1];
array[index+1] = base;
int temp = array[index];
array[index] = array[i];
array[i] = temp;
index++;
}
}
i++;
}
mySort(array, left, index-1);
mySort(array, index+1, right);
}
}
int main(){
int a[] = {1, 2, 12, 34, 46, 54, 64, 65, 76, 98,34};
mySort(a,0,10);
for(int i = 0;i<11;i++){
printf("%d\n",a[i]);
}
return 0;
}
|
八、堆排序
堆排序是比快速排序更加复杂的一种排序算法。堆排序使用到了堆这样一种数据结构。首先我们需要搞清楚什么是堆结构。堆是一种类似完全二叉树,同时又满足如下条件的数据结构:所有子节点的值总是小于(大于)父节点。所有子节点的值都小于父节点的堆叫大顶堆,所有子节点都大于父节点的堆叫小顶堆。
二叉树你应该比较熟悉,下图就是一个小顶堆的示例:
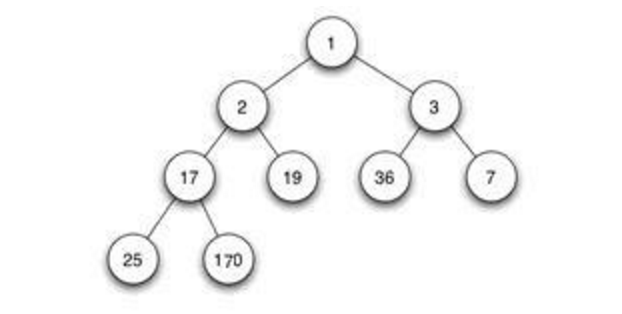
此二叉树中任何一个子节点的值都是大于父节点。如何将数列构造成这样一个堆结构呢,其实十分简单,将数列按照从上到下,从左到右的原则来构造完全二叉树即可。例如如下数列[1, 54, 2, 64, 12, 65, 76, 46, 34, 98, 34]如果将其构造成堆如下图所示:

正常情况下,这个由数组映射成的二叉树并不符合我们堆的要求,否则也就不需要我们用算法来排序了。要让这个二叉树符合要求,我们需要进行整理,即从末节点开始进行调整,例如先从12,98,34中找到最小的,放在现在12所在的位置,然后从64,46,34中找到最小的元素进行上浮,接着再一层层上浮上去,直到堆顶元素为所有元素中的最小元素。整理完成后,我们只需要将堆顶元素和最后一个元素进行交换,之后除掉最后一个元素再进行堆整理,整理完成后再将顶元素(此时为第2小)与倒数第二个元素交换,依次进行下去,即可完成数列的排序。
用文字描述堆排序步骤如下:
1.先将数列整理成符合要求的堆。
2.将首末元素交换。
3.除掉最后一个元素在进行堆的整理。
4.重复进行2和3,直到数列排序完成。
C语言实现的堆排序算法:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
| #include <stdio.h>
void store(int array[],int index,int end){
int top = array[index];
int left;
int right;
if (index*2+1<=end) {
left = index*2+1;
}else{
return;
}
if (index*2+2<=end) {
right = index*2+2;
}else{
if (array[left]>top) {
array[index] = array[left];
array[left] = top;
top = array[index];
}
return;
}
if (array[left]>top) {
array[index] = array[left];
array[left] = top;
top = array[index];
}
if (array[right]>top) {
array[index] = array[right];
array[right] = top;
top = array[index];
}
}
void mySort(int array[],int end){
int i = end;
while(i>=0){
store(array,i,end);
i--;
}
int temp = array[end];
array[end] = array[0];
array[0] = temp;
end--;
if (end>0) {
mySort(array,end);
}else{
return;
}
}
int main(){
int a[] = {1, 2, 12, 34, 46, 54, 64, 65, 76, 98,34};
mySort(a,10);
for(int i = 0;i<11;i++){
printf("%d\n",a[i]);
}
return 0;
}
|
九、归并排序
归并排序的核心并不是交换元素的顺序,而是将数列分成多个有序小数列,将相邻的小数列进行归并。文字描述归并排序步骤如下:
1.把长度为n的数列分成长度为1的n个数列。
2.相邻数列进行排序归并。
3.重复操作2,直到所有数列归并成1个整体。
C语言实现的归并排序算法:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
| #include <stdio.h>
void merge(int array[],int temp[],int start,int end,int middle){
int i=start,j=middle+1,k=start;
while(i<middle+1 && j<end+1){
if(array[i]<array[j]){
temp[k++] = array[i++];
}else {
temp[k++] = array[j++];
}
}
while(i<middle+1){
temp[k++] = array[i++];
}
while(j<end+1){
temp[k++] = array[j++];
}
for(i=start;i<=end;i++){
array[i] = temp[i];
}
}
void sort(int array[],int temp[],int start,int end){
int middle;
if(start<end){
middle = (start+end)/2;
sort(array, temp, start, middle);
sort(array, temp, middle+1, end);
merge(array, temp, start, end, middle);
}
}
int main(){
int a[] = {1, 2, 12, 34, 46, 54, 64, 65, 76, 98,34};
int b[11] = {0};
sort(a,b,0,10);
for(int i = 0;i<11;i++){
printf("%d\n",a[i]);
}
return 0;
}
|







